Validate Your Model Robustness
Saimple is a static analyzer that helps you demonstrate your model trustworthiness using formal proof, not marketing claims.
What is robustness in AI systems?
As the use of Machine Learning (Neural Networks, Support Vector Machines,…) is getting more and more prevalent, it is important to remember that mistakes happen everywhere, even among machines. The problem is, with machine learning, mistakes can be hard to detect, since the model is often perceived as a black-box. We cannot predict accurately why, when, or how often these mistakes happen, to the point where it can even remain unseen by the user.
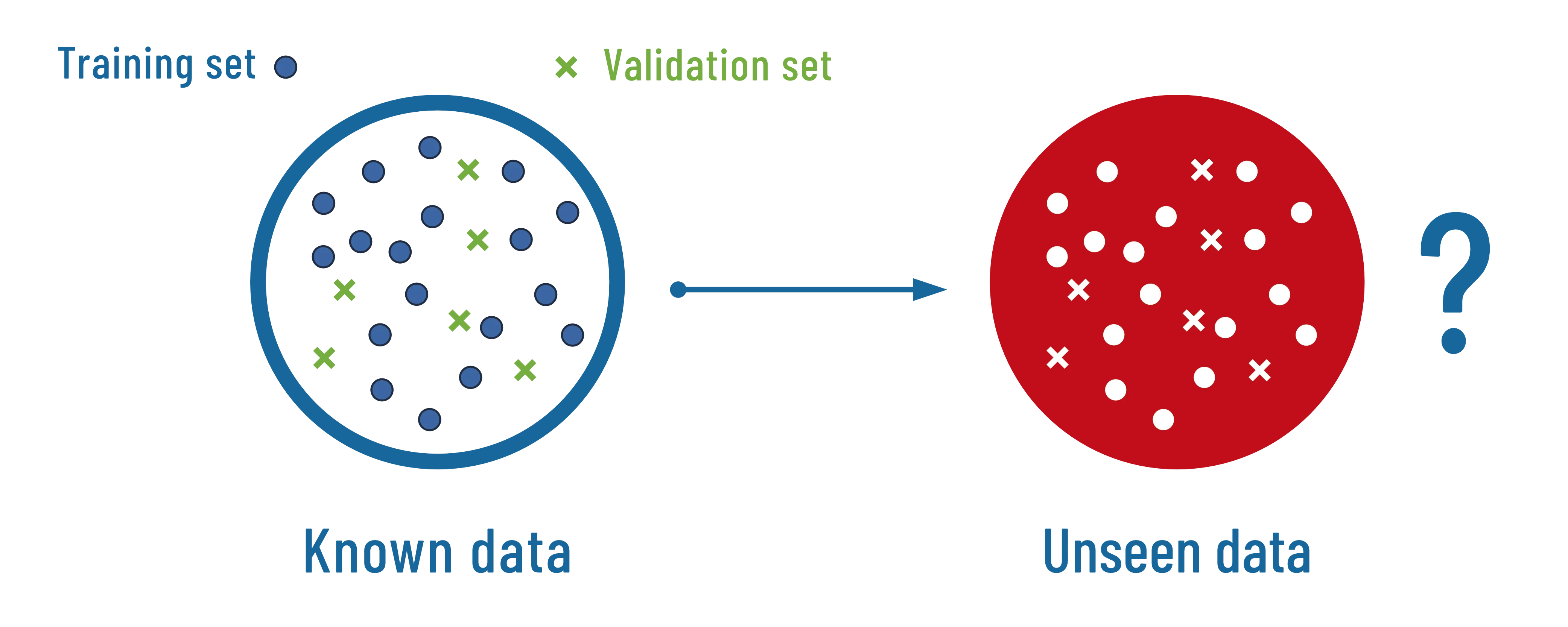
Figure 1: The training and validation data sets used to build a machine learning model are only a small subset of all the possible data
When designing their model in a supervised training way, AI engineers select two sets of known data: the training set and the validation set. But however big these sets are, most of the time, they do not cover the whole set of possible data. So what happens for the rest, the unseen data ?
In particular, what happens around a specific data point ? Or, in other words, what happens if we add some perturbations to it ? As an example, in a famous paper called Explaining and Harnessing Adversarial Examples, a team of researchers applied noise to a picture of panda and gave it for the Neural Network GoogLeNet to classify. While it was classified as a panda with 57.7% of confidence before applying the noise, afterward, it was misclassified as a gibbon with 99.3% of confidence. The surprising part is, the noise is not even perceptible to the human eye. This example is a classical adversarial example, i.e. an input specifically designed to confuse a machine learning model.
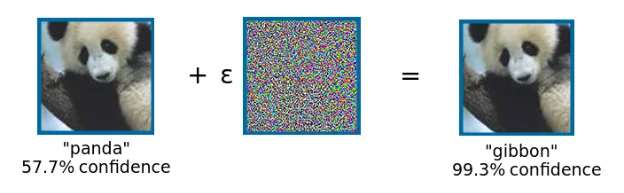
Figure 1: The training and validation data sets used to build a machine learning model are only a small subset of all the possible data
This example highlights the fact that when engineers deploy a machine learning model, they do not only need it to be accurate (before adding the noise, GoogLeNet classifies the panda accurately) , they also need it to be robust. In other words, if some selected perturbations are applied to the inputs, they need their model not to change its output. Note that the perturbations are not limited to adversarial ones, one can test the robustness on any chosen type of perturbation, such as filters on images, random noise on signals, spelling mistakes on NLP, etc.
More formally, we define the robustness of a machine learning model as its capacity to maintain its performance regardless of the circumstances. The notion of robustness is closely related to the ones of stability and sensitivity defined by the ISO standards ISO/IEC 24029-1 and ISO/IEC 24029-2. The stability of a model expresses to which degree its output remains the same when we apply perturbations to its inputs. Its sensitivity expresses how much the output changes when we change the inputs.
Why is robustness important?
Hopefully, the lack of robustness of GoogLeNet when distinguishing pictures of pandas from pictures of gibbons did not have much consequences. But in critical areas such as health, defense or transportation, introducing machine learning models that lack robustness could lead to catastrophic outcomes. To convince yourself, just imagine a self-driving car that could not spot a pedestrian whenever it was raining, or an AI that would not detect cancerous cells in a patient’s X-ray whenever it was a little bit blurry. This could be dramatic.
To prevent this from happening, some measures are currently being taken. In the EU, the AI-Act intends to regulate the use of artificial intelligence by imposing different requirements depending on how risky an AI system can be, across all sectors. In particular, in the category of high risk systems, the AI models will have to guarantee robustness to be put on the market. Some norms, certifications and qualifications are currently being defined, either horizontally (ISO/IEC, CENELEC) or in specific vertical areas such as transportation (DO178C), space (ECSS) or defense (DGA referential, NATO doctrine, EDA standardization groups). All of these come to a same conclusion (among many others): Robustness needs to be guaranteed.
How to verify robustness?
The first obvious way to guarantee the robustness of a machine learning model, i.e. its behavior with the unseen data, would be to simply apply it the unseen data. The problem is, this is most of the time impossible due to the number of data one would have to possess or generate. To give an idea, if we take a small frame of 3×3 pixels on a picture, with the R,G and B channels, and allow to apply small perturbations in this frame, between -1 and +1 (on the 256 possible values for each pixel and channel), we already obtain 327 images to test, i.e. more than 7.5 billions.
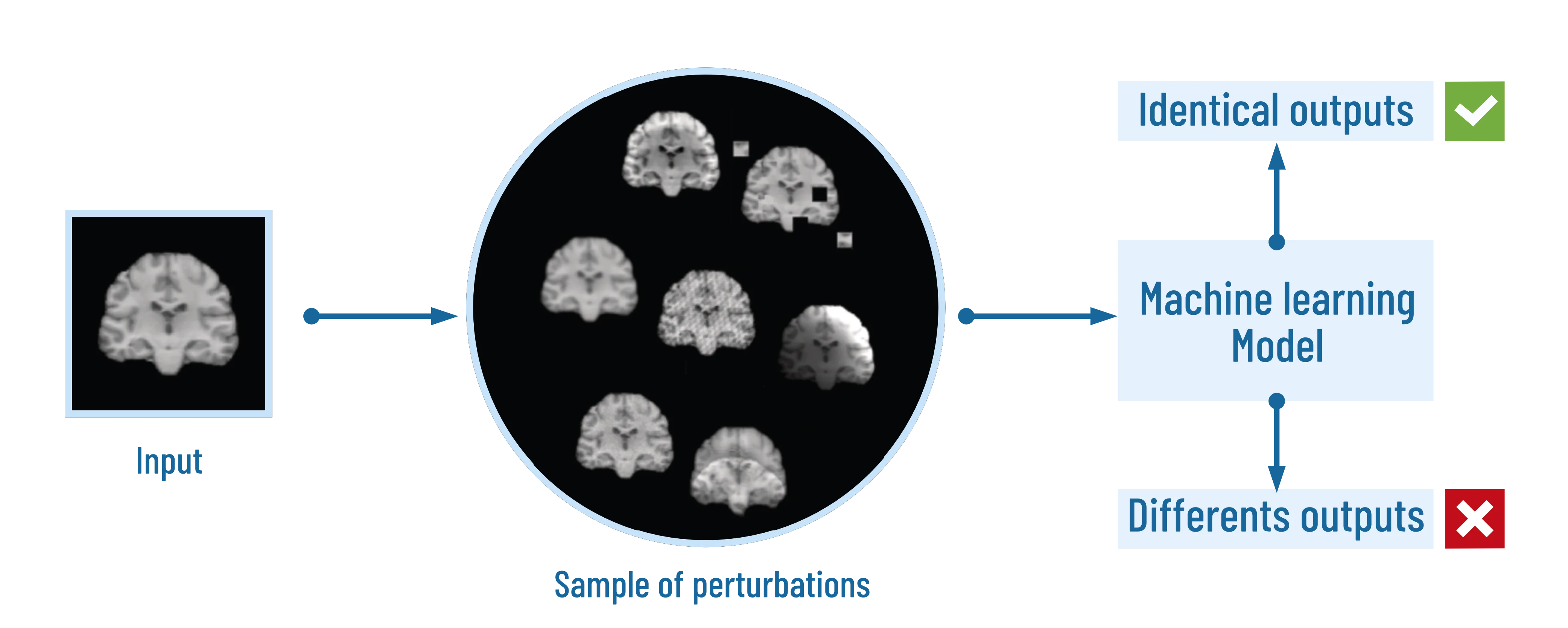
Figure 3: A first way to test a model’s robustness is to verify that its output remains identical when applying a chosen sample of perturbations. But this method does not provide a formal proof of robustness.
Reference 1: Original image on Dufumier, Benoit, et al. “Benchmarking CNN on 3D anatomical brain MRI: architectures, data augmentation and deep ensemble learning.” arXiv preprint arXiv:2106.01132 (2021).
A first way to avoid this issue consists in only testing a sample of this data. This is referred to as the statistical method. In this method, one generates a more reasonable number of perturbations and give it to the model to see if the output changes. If the output never changes, then the model is probably robust.
But is it enough to prove that a model is probably robust ? It might be sometimes, but when it comes to critical applications, is it not enough to know that the unacceptable will probably not occur. In these cases, we need an actual guarantee, a formal proof of robustness. We also say that the statistical method is not sound. A method is called sound if it necessarily detects any lack of robustness under the specified perturbations. That being said, a method that is sound is not necessarily complete. A method is called complete if it necessarily detects the robustness (under the specified perturbations) of a robust method. A method that is both sound and complete is called exact.
Recently, a lot of different sound methods have been developed in order to formally verify the robustness of neural networks. Some of them, such as Mixed-Integer Linear Programming (MILP), or Satisfiability Modulo Theory (SMT) are exact methods. However, their exactness often comes with a price, that is, they can generally verify only small neural networks and can take a lot of time to do so.
To go faster and verify larger machine learning models, one has to resort to incomplete methods. One of them, abstract interpretation, has already been successfully used in major industrial programs such as Astrée, to verify safety properties for planes, cars or even spacecrafts. The principle of abstract interpretation is the following: since it is too costly to test each possible perturbation individually, we merge them into a single abstract object, and observe mathematically how the boundaries of this object behave when passing through the model. Then, we verify if the output object is still within the intended result. If it is, then the model is proven robust. This method is sound since all of the possible perturbations are included in the object, but it is not complete. Indeed, if the robustness is not proven at the end, it does not necessarily mean that the model is not robust, since there are data points in the abstract object that do not correspond to any desired perturbation.
Saimple and the abstract interpretation framework
Saimple uses the abstract interpretation framework in order to guarantee the robustness of machine learning models such as Support Vector Machines or Neural Networks. We now give more details about the abstract interpretation method.
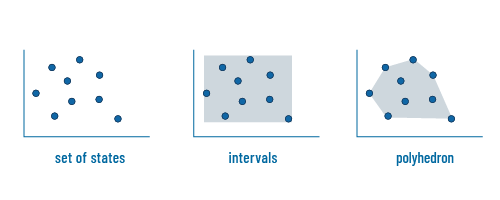
Figure 4: Sets, intervals or polyhedrons can be used to abstract a sequence of states
Abstract interpretation is a theory that was introduced in 1977 by Cousot and Cousot in their paper Abstract interpretation: A Unified Lattice Model for Static Analysis of Programs by Construction or Approximation of Fixpoints. The purpose of abstract interpretation is to approximate program semantics, and it is often used in order to make sure that a program verifies a given property. Its use is not limited to robustness issues, nor to machine learning models.
The idea is that in order to verify how a program behaves, instead of looking at the sequence of states that are reached when running the program, we approximate this sequence into one abstract object. This abstract object can take different shapes, and each of these shapes come with a certain precision and computational cost. For example, this object can be the set of states, as illustrated in Figure 4. This abstraction already gives slightly less information than the sequence of states, as we do not know in which order they appeared. One can also approximate it by looking at the minimum and maximum values of the variables, giving an interval for each of them. Note that in this abstraction, some data points (the abstract states) may not correspond to any actual reached state (the concrete states). We can also refine this abstraction by taking a polyhedron. It is more precise, as there are less abstract states that are not concrete states, but it makes the property harder to compute. As mentioned above, when choosing the shape of the abstraction, there is a trade-off to consider between precision and speed.
In Saimple, we approximate the set of all possible perturbations into a single abstract input object. Then, we observe the behavior of this object when it passes through the machine learning model. In particular, when dealing with neural networks, we observe how the object changes layer by layer, and even operator by operator, as illustrated in Figure 5. For that, Saimple has to support a lot of different activation functions, including non linear functions, such as the sigmoid or the hyperbolic tangent functions. But with non linear functions, computing the image of the object is not always straightforward. For this reason, we sometimes have to approximate the functions. As long as we take the induced error into account, so that the obtained image object includes all the actual images of the input object, the method stays sound.
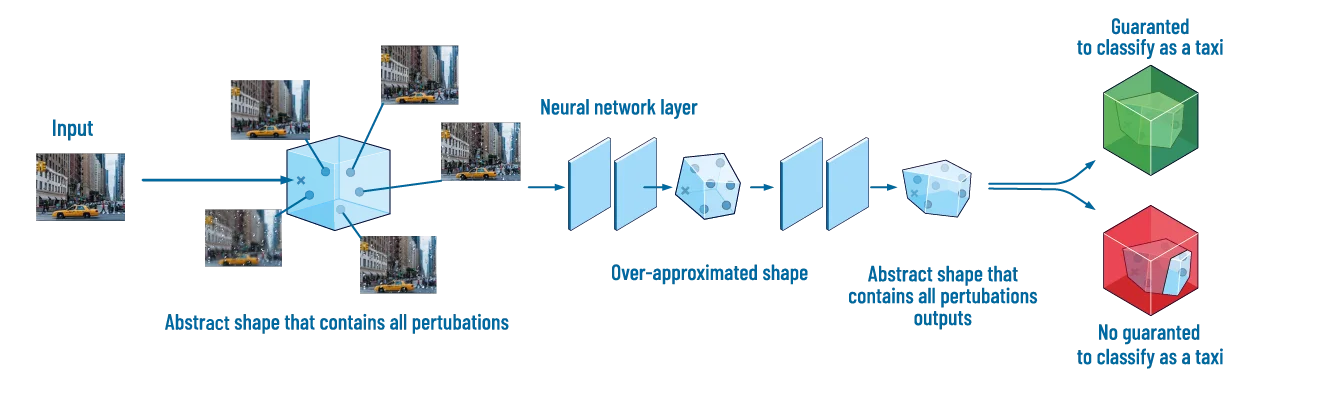
Figure 5: To formally prove the robustness of a neural network model, Saimple use abstract interpretation through all the neural networks layers.
Computing the abstract image objects layer by layer finally gives an abstract output object. This object is what we use in order to verify if the machine learning model is robust. For example, for a classifier machine learning model, the model typically outputs a score for each class, then selects the class with highest score. In this case, what Saimple does is output an abstract object for each of the scores. Then, it verifies if the object with highest maximum score intersects any other object, as illustrated in Figure 5. If it intersects, then we cannot guarantee robustness. Note that it does not necessarily mean that the model is not robust (as previously mentioned, the abstract interpretation method is not complete), as we cannot know if the intersection is caused by a state that is actually reached by the program, or if it is due to the over-approximations. On the contrary, if there is no intersection, Saimple provides a proof of robustness. Indeed, the absence of intersection means that the class with higher score is the same for all considered perturbations. We say that this class is dominant. The notion of dominance is closely related to the one of maximum stable space. The maximum stable space of a model, defined in the ISO standard ISO/IEC 24029-1, correspond to the input space in which it is possible to prove dominance.
As previously mentioned, this method is sound, but not complete. Indeed, by construction, due to the abstractions and over-approximations, Saimple cannot assess that your machine learning model is not robust. What Saimple can do, however, is guarantee your model’s robustness, and it does it on very large machine learning models, with short computation time, thanks to the approximations. This makes it the perfect tool to help in designing your machine learning model, verify your training data, and to finally make sure that your model is robust enough to be put on the market.